My love of snail shells did not begin at a young age. This is not a story of a 6-year old boy discovering his first shell on an idyllic sandy beach. The year was 1998. I was 23 and in the first semester of graduate school. I was not sitting in the sand with the smells and sounds of the ocean washing over me. Instead, I was surrounded by the cement, cinder block walls of an interior lab of a architecturally emotionless university during a harsh Boston winter. Yet here, I was inspired by two papers from the 1960’s by David Raup, demonstrating that the shape, and beauty, of a snail’s shell could be described mathematically. From these papers my love of snail shells, and eventually mollusks in general, blossomed.
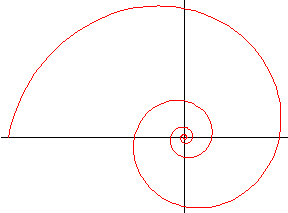 Snail shells have a very important feature—they spiral logarithmically. This feature was noted Greek philosophers, Christopher Wren, and expounded on in depth in 1917 by D’Arcy Thompson in his seminal book On Growth and Form. In a very crude sense, these early tomes provide the first steps into actually representing the entirety of a shell’s shape with numbers. Raup in the 1960’s devised a model with four parameters that went far beyond a simple line drawing in a single plane (Raup 1961, Raup 1962, Raup 1966).
Snail shells have a very important feature—they spiral logarithmically. This feature was noted Greek philosophers, Christopher Wren, and expounded on in depth in 1917 by D’Arcy Thompson in his seminal book On Growth and Form. In a very crude sense, these early tomes provide the first steps into actually representing the entirety of a shell’s shape with numbers. Raup in the 1960’s devised a model with four parameters that went far beyond a simple line drawing in a single plane (Raup 1961, Raup 1962, Raup 1966).
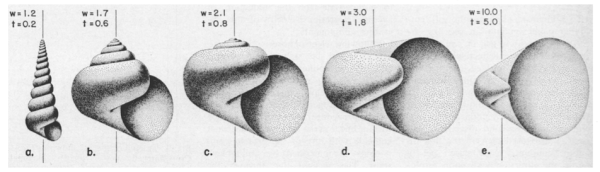
 The first parameter was the shape of the generating curve. Imagine a tube of Play-Doh extruded from press. We could have a different mold to give this tube different shapes and ridges. This is the shape of the generating curve.
The first parameter was the shape of the generating curve. Imagine a tube of Play-Doh extruded from press. We could have a different mold to give this tube different shapes and ridges. This is the shape of the generating curve.
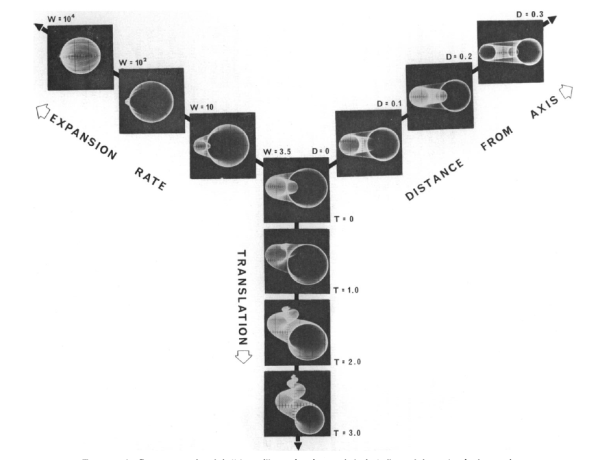
 The next parameters deal with the actual spiraling of this tube. If the tube is bent around an axis, how far does this tube move away from the axis with each turn? This is the variable D, the distance from the axis. If the value is zero then tube produces a coiled cylindrical shell, similar to the shells just above, but if the value is greater than zero the shell gets a little wider with each whorl becoming triangular.
The next parameters deal with the actual spiraling of this tube. If the tube is bent around an axis, how far does this tube move away from the axis with each turn? This is the variable D, the distance from the axis. If the value is zero then tube produces a coiled cylindrical shell, similar to the shells just above, but if the value is greater than zero the shell gets a little wider with each whorl becoming triangular.
The third value, W, is the whorl expansion rate expressing how much the tube’s diameter increases as it spirals. The fourth, T, is the translation rate quantifying how that tube moves vertically (D is the horizontal movement) with each subsequent whorl. Nowhere are these parameters better explained than in Raup’s original work.
But the true beauty of Raup’s model was that each species could have its own unique set of parameter values.
 You can envision calculating the values for D, T, and W for each snail and plotting them in a three-dimensional space with the axes corresponding to Raup’s parameters. If we did this would some parts of this space be uninhabited?. As stated by Raup himself,
You can envision calculating the values for D, T, and W for each snail and plotting them in a three-dimensional space with the axes corresponding to Raup’s parameters. If we did this would some parts of this space be uninhabited?. As stated by Raup himself,
Do the relatively unused regions represent physiologically impossible shell forms or has the evolution of these taxa simply not had sufficient time in which to populate the entire [region]?
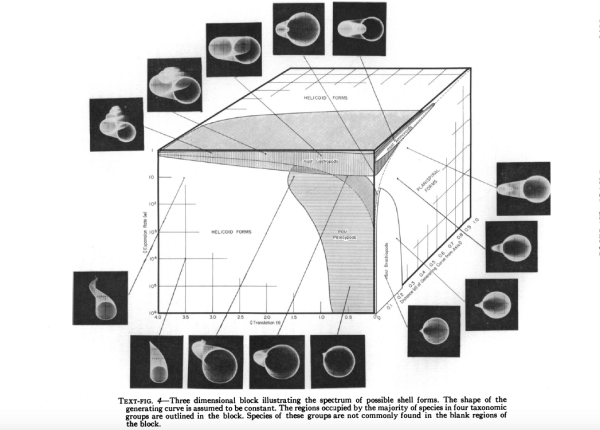 In doing this, Raup had launched a new courses of study focused on using both mathematical models to explore organismal shape and where organisms did and did not exist in these spaces. We now refer to these spaces in which species can be placed as morphospaces. These morphospaces can be any number of dimensions and defined by the different metrics of the morphology of an organism.
In doing this, Raup had launched a new courses of study focused on using both mathematical models to explore organismal shape and where organisms did and did not exist in these spaces. We now refer to these spaces in which species can be placed as morphospaces. These morphospaces can be any number of dimensions and defined by the different metrics of the morphology of an organism.
David Raup passed away last Thursday after a long, productive, and inspiring career. His research on extinctions and biodiversity are heralded as transformational in the field of paleontology. What will receive less attention, but touched me the most, was his little model to measure the shape of snails. Raup’s snail model papers inspired a wide diversity of research after including: how crinoids have occupied different regions of their morphospace through time, how coral growth and branching can be mathematically modelled, morphospace recovery after extinctions in ammonoid, and more complex representations of shell shape.
 Raup’s papers even inspired one intrepid, young graduate student holed up in lab to explore how the deepest parts of the oceans impact shell shape. This project that took me several years and found me x-raying millimeter size shells so I could see internal growth patterns to parameterize Raup’s variables. Years ago while visiting the University of Chicago, Raup’s old stomping grounds, I noticed the same print on several of the graduate students’ and postdoctoral fellows’ walls. I of course was drawn to the image with mouth agape. The images were original prints from the negative of figure four from Raup’s 1966 paper—the shell morphospace. Multiple prints were found in box in the department long after Raup had retired. I still covet those prints immensely.
Raup’s papers even inspired one intrepid, young graduate student holed up in lab to explore how the deepest parts of the oceans impact shell shape. This project that took me several years and found me x-raying millimeter size shells so I could see internal growth patterns to parameterize Raup’s variables. Years ago while visiting the University of Chicago, Raup’s old stomping grounds, I noticed the same print on several of the graduate students’ and postdoctoral fellows’ walls. I of course was drawn to the image with mouth agape. The images were original prints from the negative of figure four from Raup’s 1966 paper—the shell morphospace. Multiple prints were found in box in the department long after Raup had retired. I still covet those prints immensely.





My first paying gig as a programmer in the late ’70s was working for Leicester University, writing a program to draw (on a line printer!) shells based on Raup’s model. Rest in peace, Mr Raup,
You might be interested to know that Dave Raup (my husband) continued in retirement using with the mathematics of his coiling models to create beautiful computer-generated art work. View the same at Imagekind.com.